モンテカルロ法(Monte Carlo)という乱数シミュレーションを使って、投資信託の将来成績を予測する方法を紹介します。
「モンテカルロ法とは」みたいなところは他の専門サイトを参照してください。
乱数シミュレーションは資産運用の世界でもよく利用されており、例えば以下の投資シミュレーションもモンテカルロ法に基づくと記載されています。
投資シミュレーション | 明治安田アセットマネジメント株式会社
以下では乱数シミュレーションでいかに将来の運用成績を予測できるのかを紹介します。
[スポンサーリンク]
投資に利用する
例えば、インデックスファンドを用いた運用の場合、将来予想される成績は、ほぼアセットアロケーション(資産配分)で決まるとされています。
このアセットアロケーションの予想される成績は、資産の毎年の平均利回りである「リターン」と、利回りの触れ幅を表す「リスク(標準偏差)」で表されます。
ここから予想される成績を算出するには、リターンの分布が正規分布になると仮定し、モンテカルロ法を用いて大量の乱数を生成し、毎年の成績を生み出してやればよいのです。
エクセルで再現するには
モンテカルロ法をエクセルで利用するためには、NORMINV関数を利用します。
Excelを使った正規分布する乱数の生成 | 大人になってからの再学習
ここでは「=NORMINV(RAND(),平均リターン,平均リスク)」で毎年のリターンを生成し、それを運用金額にかけることでその年の運用成績を算出します。
なので、インプットに必要なデータは「リターン(利回り)」と「リスク(標準偏差)」です。
これは株価から自前で求めることもできますが、myINDEXのようなサイトのデータを借用するのが簡単だと思います。
乱数シミュレーションで将来の成績を予測するまでの流れ
まず指数(インデックス)の成績を探す
例えば、TOPIXの過去30年実績(2017年4月26日現在)は、以下のように表されます。
- リターン:0.5%
- リスク:19.4%
1980年以降の1年ごとの年次リターンが下記の図です。
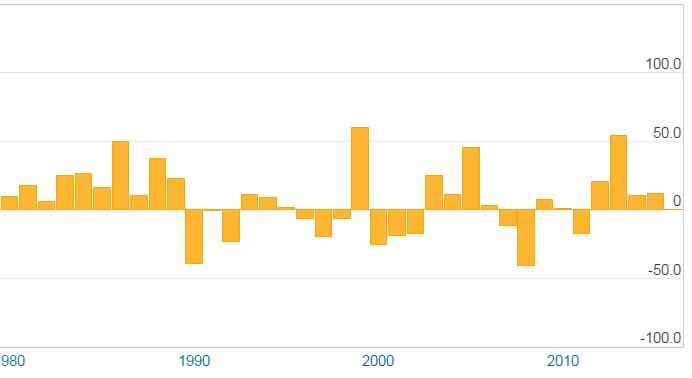
出典:http://myindex.jp/data_i.php?q=TS1047JPY
バブル崩壊が始まった1990年以降は、どちらかと言えばマイナスリターン(下に振れる)になった年が目立ちますね。
指数の成績を乱数で再現する
では、このリターン0.5%、リスク19.4%を乱数で再現します。
エクセルでこの数式にこのリターン・リスクをそれぞれインプットすると、その年の「成績」が出てきます。
毎年のリターンはリターン0.5%を中心にした正規分布になると仮定し、今後30年間の成績を算出したものが以下のグラフです。
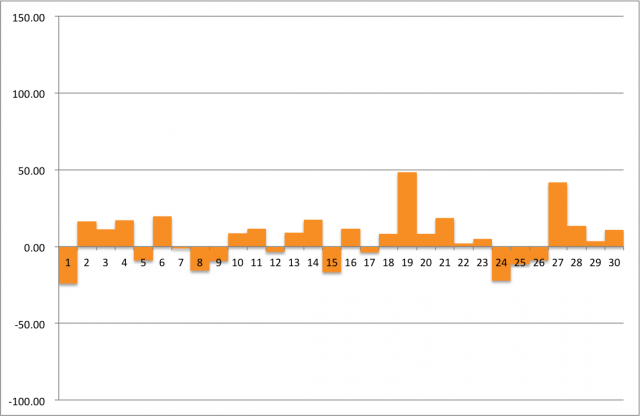
出典:筆者作成
どうです?TOPIXのこれまでの実績と似ていると思いませんか?
あとはこの年次リターンの商品に投資したと考えて、最終的な成績を算出します。
ただ、この1回の計算だけで全てを代表することはできないため、計算回数を増やすことで精度を高めます。その結果、おおよそ出現しやすい成績と、上振れ・下振れした成績が出てきます。
注意点:将来の成績を予測できないケース
モンテカルロ法は「過去の事象がそのまま将来も起こる」という前提に立つため、過去の事象が将来発生しなくなったら、乱数予測は外れます。
例えば、バブル崩壊前の日本株式の年平均リターンは6.7%だった(下記記事参照)のに対して、バブル崩壊後のTOPIXの過去30年の年平均リターンは0.4%でした。
130年間の超長期株価チャートから分かること | The Capital Tribune Japan
この状況下で、モンテカルロ法に利回り6.7%を設定すると、当然高い期待リターンが求まります。しかし、現実とはちょっと乖離が大きいかもしれませんね。
このように、この乱数計算が過去の成績に依存している点に注意してください。
[スポンサーリンク]
まとめ
- 投資・資産運用で将来の成績を予測する際に乱数シミュレーション(モンテカルロ法)は参考データとして利用できる
- 投資の成績をエクセル上で再現するなら「=NORMINV(RAND(),平均リターン,平均リスク)」
- 将来は過去と同じトレンド上にあるとは限らない点に注意。この計算は「将来は過去と変わらない」との前提に立つ
所詮は数字のお遊びなので、おまけとしてご覧になるのが良いと思います。
モンテカルロ法の結果は良い道しるべになると思います。が、その道は必ずしも正しい道とは限らない点に留意すべきです。
将来の成績を予想する方法は他にもありますので、合わせてご覧ください。

モンテカルロ法の他の記事はこちらから。

