つみたてNISAで商品を運用する際には、その商品の予想される利回りがどのくらいか、という計算はよくやります(東北投信でもよくやっています)。
というのも、アセットアロケーションさえ決まれば、過去の利回りがいくらだったかが求まりますので、その数値を金利計算ツールに入力すれば、将来得られそうな利益も決まる、という話です。
ただ、その平均的な利回りを多くの人が享受できるかはどうも怪しい、というのがここでの本題です。
多重回の計算を行なう限り、多くの人は理想的な複利の運用結果よりも悪くなる可能性があります。
書いてる意味が分かりにくければ、まあ記事をざっと読んでいってください。
なお、予め書いておくと、筆者知識がまだ追いついてないので、この話は将来的にまだまだ続けることにしておきます。
[スポンサーリンク]
乱数シミュレーションにて、平均値と中央値を求める
前提条件
いつものモンテカルロシミュレーションにて平均値と中央値を求めます。
このツールは筆者作成のもので、投資信託の運用成績が正規分布することを前提に作っているものです(厳密には、投資信託の運用成績は正規分布になりません)。
なお、エクセル上の複利計算は、
毎年の積立額 × (((1 + その年の利回り) ^ 運用年数) – 1) / その年の利回り
で求めており、利回り部分を乱数発生にて毎回成績を変える感じです。
計算条件:外国株式にありそうな成績を1万回計算する
今回、以下の条件で1万回計算を行ないました。
- リターン:6%
- リスク:18%
- 積立額:毎月1万円
- 運用年数:20年
この成績は外国株式(先進国株式)の運用成績として、よくありそうなものです。
シミュレーション結果
見込まれる運用成績の中央値は平均値よりも低い
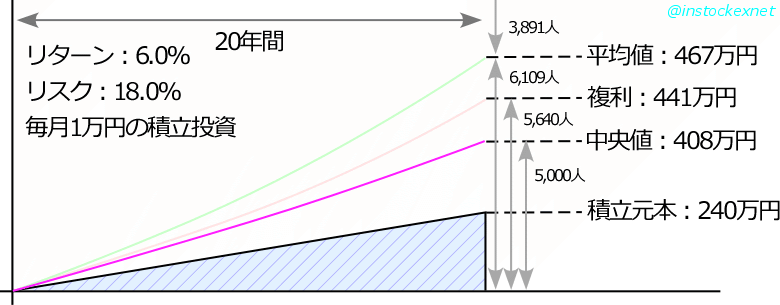
この条件で計算を行なうと、以下のような結果が得られます。
- 理想的な複利(リスク0で運用した場合):441万円
- 平均値:467万円(1万回の平均)
- 中央値:408万円(5,000番目に来るデータ)
年収の統計に関心がある方ならご存知かと思いますが、中央値と平均値はちょっと違う意味を持つデータです。
「平均値」は、「データを足し合わせ、データの個数で割った値」のこと。 「中央値」は、「データを小さい(または大きい)順に並べ、真ん中に来る値」のこと
今回の計算では、中央値は平均値やリスクゼロで運用した理想的な複利よりも低くなっています。
つまり、過半数のデータは平均値・リスクゼロで運用した理想的な複利よりも低い側にあります。
人数ベースで考えると
これを人数ベースで考えると以下のようになります。
なお、計算回数は1万回なので1万人の運用成果として考えます。
1万人が毎月1万円をリターン:6%、リスク:18%の商品に積立投資した場合
- 平均値である「467万円」以上の成績になる人:3,891人
- 理想的な複利の運用成績である「441万円」にならない人:5,640人
- 中央値である「408万円」にならない人:5,000人
- 元本割れで終わる人:1,455人
下記記事でシミュレートしたように、投資信託の運用成績はここまで簡単な話にはなりません。
が、計算上、多くの人は期待される複利以下の成績で終わってしまう可能性があります。
車輪の再発明である理由
この話、実は10年ぐらい前にもブログ界隈で話題になったことがあります。
この投資信託を5年保有したとき、そのリターンは平均すれば10%の5年複利と同じ結果が期待できる。ただし、結果の半数以上は複利以下の結果であることはほぼ間違いない、平均が複利に追いついているのは、わずかな確率だが大儲けできる可能性があるからだ
筆者は最近まで知りませんでしたw
つまり、こういうことである
過去の利回りを用いた計算から求まる予想利益を見てうっとりするのはやめましょう、という話です。
ここまでの話は、過去の利回りから将来の予想利益を求めることができるが、確率的にその利回りには達しない可能性がある、というものでした。
ちなみに、運用年数が長くなるほど、「理想的な複利の利回り」には届かなくなる可能性が高いです。
将来の予想成績を考える際には、「過去の利回り – 1%」ぐらいで見積もるのが良いのかもしれませんね。
[スポンサーリンク]
まとめ
- 毎年の利回りが正規分布になることを前提に、1万回の運用シミュレーションを行なった
- その結果、多重回の複利計算を行なうと、得られる結果の半数はリスクゼロで見込まれる複利以下の運用成績になる
- 将来の運用成績を予想するときは、少し控えめな利回りで計算したほうが良さそう
本でも読んで勉強してきますわw
自分自身の将来の運用も後でちょっと見直そうって気になってきました。
また新たなことを学んだら記事にて紹介します。
