今回は全世界株式に投資する時に、GDP比率で投資するか一般的な時価総額比率で投資するかの比較を行いました。その結果、GDP比率で投資する全世界株式は、新興国株式の比率が多くなるため、ややハイリスクハイリターンな特徴になることを紹介します。
将来的にGDPと時価総額比率のどちらが良いかは「神のみぞ知る」ところですが、この比較においては、個人的には時価総額比率(つまり、オール・カントリーなど)で十分だと思ってます。
なお、他の全世界株式の記事は以下よりご覧ください。

では、一緒に詳しく見ていきましょう!
[スポンサーリンク]
時価総額比率との資産配分の違い
一般的な時価総額加重比率のアセットアロケーションと、GDP比率のアセットアロケーションでは主に先進国株式と新興国株式の組み入れ比率が違います。
| 株式 | 時価総額加重比率 | GDP比率 |
|---|---|---|
| 日本 | 7% | 6% |
| 先進国 | 81% | 54% |
| 新興国 | 12% | 40% |
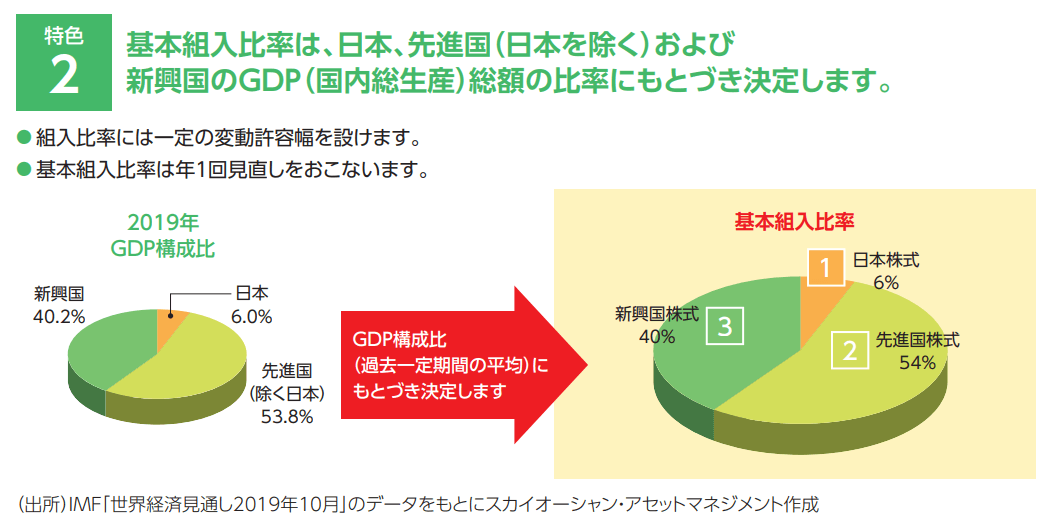
以下はGDP比で全世界株式に投資する「グローバル株式ファンド(The GDP)」のアセットアロケーション。

出典:https://www.soam.co.jp/file/100010100010/100010_moku_k.pdf
次に時価総額比率で全世界株式に投資するオール・カントリーのアセットアロケーションです。
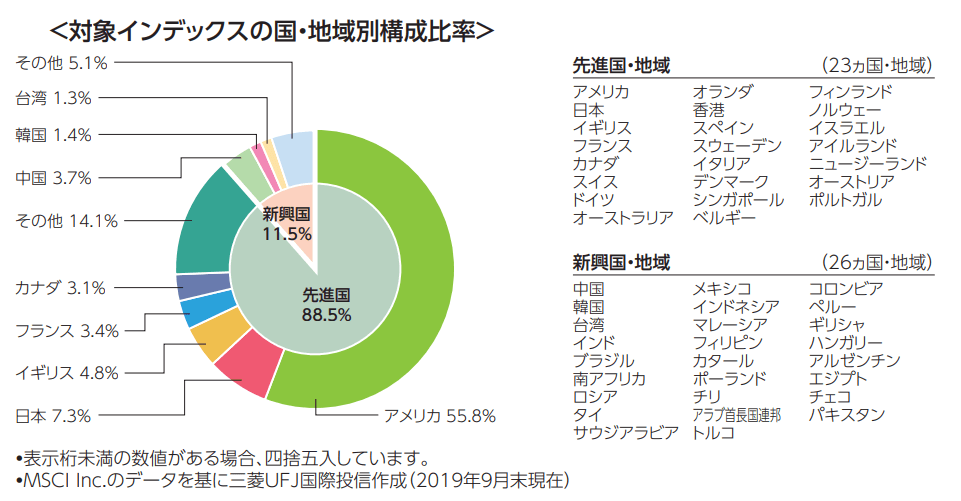
出典:https://emaxis.jp/pdf/koumokuromi/253425/253425_20200125.pdf
時価総額加重比率の全世界株式は資産配分の大部分が先進国株式(というか、米国株式)になるのに対し、GDP比率の場合には新興国株式が40%占める点で特徴的です。
GDP比率を選ぶ判断のポイント
解釈の違い
単刀直入に言えば、現在の株価は正しくない(新興国株式が過小評価されている or 先進国株式が過大評価されている)と考えるなら「GDP比の全世界株式」を選びます。一方、先進国株式も新興国株式も、現在の株価は正しいと考えるなら「時価総額の全世界株式」を選ぶことになります。
インデックス投資のベースにあるのは「現代ポートフォリオ理論」です。現代ポートフォリオ理論では「時価総額加重比率(時価加重ポートフォリオ)」は現在の株価が正しいことを前提にしています。
一方、GDP比率とは新興国株式の株価が過小評価されている(or 先進国株式の株価が過大評価されている)という判断を加えたことになります。つまり世界経済の規模に対して、株価が釣り合っていないため、経済の規模に合わせたのがGDP比の全世界株式です。
出典:https://www.nikkoam.com/files/pages/institutional/pdf/investment_insight_series/investment_insight_series_201308_02.pdf
新興国株式を重視すること
結局のところ、この話は新興国株式に投資は必要なの?という話に着地します。一般的な全世界株式ファンドよりも新興国株式を多めに保有するのですから、「なぜ新興国株式を多めに持つか」という理由が必要になると思うのです(下記記事参照)。

過去のパフォーマンスを見る限り、新興国株式は価格変動の大きい市場です。
GDP比で全世界株式に投資する「MSCI ACWI GDP Weighted」によれば、時価総額比率の全世界株式に比べ、リターンもリスクも高まっています。その点で、GDP比率の全世界株式ファンドは上級者向きに感じます。
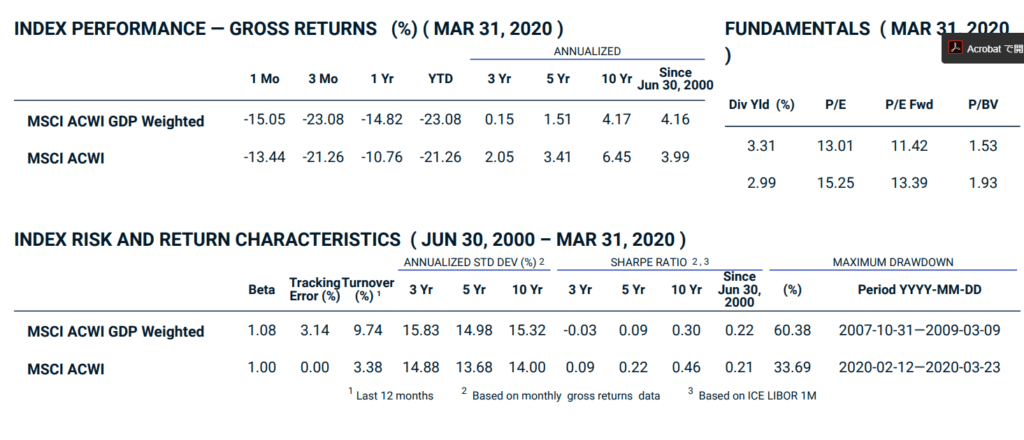
出典:https://www.msci.com/documents/10199/a195824c-2ec7-488b-96c2-7d840a7a9186(pdf)
これらを勘案すると、普通の時価総額比率の全世界株式ファンドでもよいかなと思うところです。すなわち、グローバル株式ファンド(The GDP)よりかはeMAXIS slim 全世界株式(オール・カントリー)やたわらノーロード全世界株式でよい、という判断です。
なお、新興国株式が必要かどうかについては、下記記事も参照になさってください。

[スポンサーリンク]
まとめ
- 一般的にGDP比率で全世界株式のアセットアロケーションを作ると、新興国株式の割合が多くなる
- GDP比率のポートフォリオは経済の規模に対して、ある国や地域の株価の評価が過小であるとの判断に基づく
- 新興国株式の割合が多くなると、ハイリスクハイリターンになりやすい。大きな価格変動に耐えられる上級者向けの商品になる
ちなみにリーマンショック以前は新興国株式が高いパフォーマンスを出していました。その時であれば、現在以上にGDP比率の全世界株式は興味を持たれたかもしれませんね。
他の全世界株式の記事は以下よりご覧ください。

ちなみに新興国株式のインデックスについては、以下の記事でも解説しています。